La paradoja del seguimiento de reglas
I
En algún momento de nuestras vidas nos cruzamos o hemos hecho algún test de inteligencia, ya sea en la escuela o por mera curiosidad. La mayoría de los test tienden a plantear problemas lógicos en los cuales, al dar una respuesta predeterminada, nos dará un puntaje final que medirá nuestro coeficiente intelectual. Como dije la respuesta en estos test es una sola, es acertar por completo o errar por completo.
Un problema interesante en estos tests surge cuando hay respuestas que no son correctas, respuestas que no dudaríamos en marcar como erradas, pero que sin embargo pueden argumentarse como una solución alternativa, una solución que se desvía de la norma y que nos vemos obligados a aceptar también como correctas a la luz de la razón ¿Como se explica este fenómeno?
II
Wittgenstein planteo el problema de seguir una regla en varios de sus escritos póstumos. En el libro Investigaciones Filosóficas es donde nos encontramos con la formulación explicita de la paradoja. En el pasaje 201 de ese libro dice lo siguiente:
«Nuestra paradoja era ésta: una regla no podia determinar ningún curso de acción porque todo curso de acción puede hacerse concordar con la regla».
La paradoja es bastante clara: La regla en sí misma no nos da un camino explicito para seguir una serie, la continuación puede ser distinta de la esperada y sin embargo ser acorde con la regla. En el caso de los tests de inteligencia, una solución alternativa al problema lógico que a primera vista parece errónea, puede ser válida y ajustarse al problema adecuadamente.
Hay dos autores que a mi forma de ver popularizaron esta paradoja, de distinta manera y en distintos campos. Uno es el novelista bahiense Guillermo Martínez y el otro el filósofo Saul Kripke.
III
La paradoja del seguimiento de reglas es un tema recurrente en la obra de Martínez. En especifico se la menciona en el capítulo 9 de Crímenes Imperceptibles (además de que es uno de los puntos de reflexión a lo largo de la novela), el capítulo 28 de Los Crímenes de Alicia y en la entrada de su blog personal Series lógicas y crímenes en serie. Martínez logra combinar en estos trabajos conceptos de la novela policial con filosofía de las matemáticas de manera magnifica, por lo cual es mas que recomendable su lectura.
Ahora bien, la finalidad didáctica de la paradoja en la obra de Martínez es mostrar como una serie de símbolos (o como el la denomina, una serie lógica) puede tener múltiples continuaciones que se ajustan a la regla. Martínez llama la atención en que al elegir un camino por sobre otro pueden primar criterios como la «simplicidad» o la «elegancia» de la solución.
El ejemplo que suele utilizar es la siguiente serie:
2, 4, 8, 16, ?
Intuitivamente nos parecería indicar que la serie continuaría con el número 32, ya que parece que estamos multiplicando los números de la serie por dos. Pero Martínez nos dice es posible (y razonable) seguir la serie con otro número como 31 (Para el lector interesado, la demostración de esto se encuentra en la entrada del blog ya mencionada). Por otra parte Martínez también menciona un teorema matemático que parece dar sustento a la paradoja de Wittgenstein: El teorema de interpolación de Lagrange. Citando textualmente una nota al pie en el capítulo 28 de Los Crímenes de Alicia, dice lo siguiente: «(…) Y para la continuación de la serie 2, 4, 8, 16 con un número n cualquiera, el teorema de interpolación de Lagrange asegura que hay un polinomio P(x) tal que P(1)=2; P(2)=4; P(3)=8; P(4)=16; P(5)=n.»
IV
Saul Kripke en su libro Wittgenstein: A Propósito de Reglas y Lenguaje Privado hace una interpretación de la paradoja que también se encontraría dentro del marco de la filosofía de la matemática de Wittgenstein, pero la extiende ya que la ve como un tipo de argumento escéptico. Kripke nos plantea la siguiente situación: Supongamos que conocemos como utilizar la función sumar. A lo largo de nuestra vida sumamos una cantidad finita de veces pero la regla nos permite sumar una cantidad indefinida, con resultados que no antes tenía previstos. La cuestión es sencilla, al aprender a sumar capto una regla y mis usos pasados de la regla me permiten llegar a una única respuesta en una cantidad indeterminada de casos futuros donde tenga que aplicarla. Ahora supongamos que yo nunca sume los números «68+57». Aplicando la regla, obtendría como resultado el número «125» y cualquier profesor me diría que es correcto. Sin embargo un escéptico me diría que estoy equivocado, que la solución a la suma «68+57» en realidad es «5». Nos argumenta que en el pasado, lo que yo entendía por sumar o mas era en realidad la función cumar o cuas y que se define de la siguiente forma:
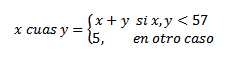
El escéptico sostiene que malinterpreto mi uso previo ya que cuando decia x mas y, en realidad quería decir x cuas y. Kripke nos dice lo siguiente: No hay un hecho en mi historial pasado del uso de la regla que determine que «125» es la respuesta correcta ¡Quizá estuve cumando todo este tiempo sin saberlo! Por otra parte tampoco hay nada que me justifique dar una respuesta por sobre otra. La paradoja no inclinaría la balanza a favor de ninguna solución.
V
Kripke se inclina por presentar la paradoja de las reglas como un argumento escéptico y de hecho puede verse que también en Martínez se presenta una forma de escepticismo (por ejemplo si cualquier serie de números puede concluir de cualquier forma ¿Cómo es posible aprender en la escuela?). En su libro, Kripke nos muestra posibles soluciones a la paradoja, pero no me voy a detener en eso. En cualquier caso, la paradoja arroja resultados interesantes dentro de la filosofía de las matemáticas que son dignos de estudiar.
Referencias:
Kripke, Saul (1982) Wittgenstein: A Propósito de Reglas y Lenguaje Privado, Ed. Tecnos.
Martínez, Guillermo (2003) Crímenes Imperceptibles, Ed. Planeta.
Martínez, Guillermo (2012) Series lógicas y crímenes en serie en http://guillermomartinezweb.blogspot.com/2012/09/series-logicas-y-crimenes-en-serie.html
Martínez, Guillermo (2019) Los Crímenes de Alicia, Ed. Planeta.
Wittgenstein, Ludwig (1953) Investigaciones Filosóficas, Ed. Gredos.
Soy estudiante de filosofía en la UNS. Trabajo con lógica y filosofía de la ciencia.

